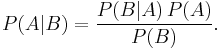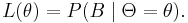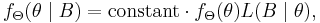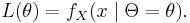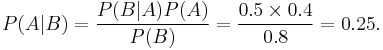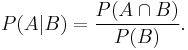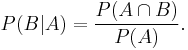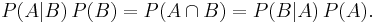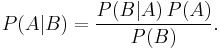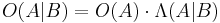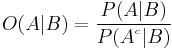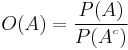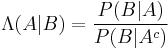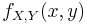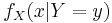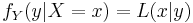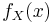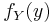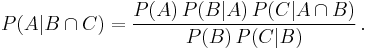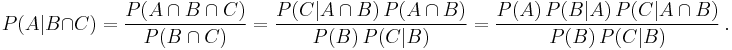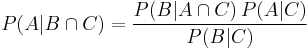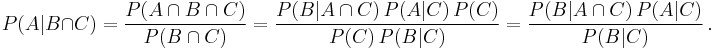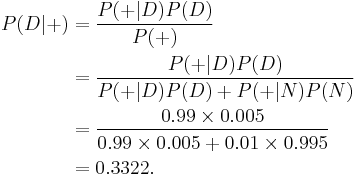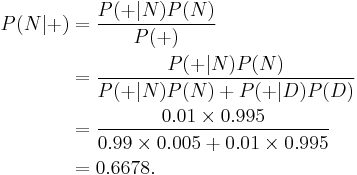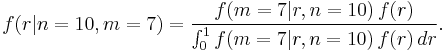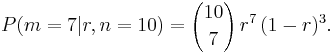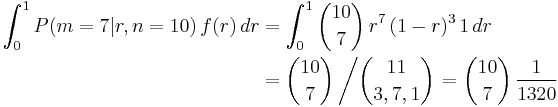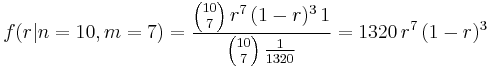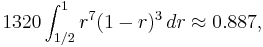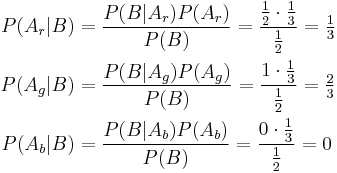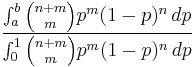Bayes' theorem

In probability theory and applications, Bayes' theorem shows the relation between a conditional probability and its reverse form. For example, the probability of a hypothesis given some observed pieces of evidence and the probability of that evidence given the hypothesis. This theorem is named for Thomas Bayes (pronounced /ˈbeɪz/ or "bays") and often called Bayes' law or Bayes' rule.

The key idea is that the probability of event A (e.g., having breast cancer) given event B (having a positive mammogram) depends not only on the relationship between A and B (i.e., the accuracy of mammograms) but on the absolute probability (occurrence) of A not concerning B (i.e., the incidence of breast cancer in general), and the absolute probability of B not concerning A (i.e. the probability of a positive mammogram). For instance, if mammograms are known to be 95% accurate, this could be due to 5.0% false positives, 5.0% false negatives (missed cases), or a random mix of false positives and false negatives. Bayes' theorem allows one to calculate the exact probability of having breast cancer, given a positive mammogram for any of these three cases, because the probability of B (a positive mammogram) will be different for each of these cases. It is worth noting that if 5.0% of mammograms result in a positive result, then the probability that an individual with a positive result actually has cancer is rather small, since the probability of the cancer is closer to 1.0%. The probability of a positive result is then five times more likely than the probability of the cancer itself. This shows the value of correctly understanding and applying Bayes' mathematical theorem.

In more technical terms, Bayes' theorem expresses the posterior probability (i.e. after evidence E is observed) of a hypothesis H in terms of the prior probabilities of H and E, and the probability of E given H. It implies that evidence has a stronger confirming effect if it was more unlikely before being observed.^[1] Bayes theorem is valid in all common interpretations of probability, and it is commonly applied in science and engineering.^[2] However, there is disagreement between frequentists, Bayesian statisticians, subjective statisticians, and objective statisticians regarding the proper implementation and extent of Bayes' theorem.

Simple statement of theorem

Thomas Bayes gave a special case involving continuous prior and posterior probability distributions and discrete probability distributions of data, but in its simplest setting involving only discrete distributions, Bayes' theorem relates the conditional and marginal probabilities of events A and B, where B has a non-vanishing probability:

$P(A|B) = \frac{P(B | A)\, P(A)}{P(B)}.$

Each term in Bayes' theorem has a conventional name:

P(A) is the prior probability or marginal probability of A. It is "prior" in the sense that it does not take into account any information about B.
P(A|B) is the conditional probability of A, given B. It is also called the posterior probability because it is derived from or depends upon the specified value of B.
P(B|A) is the conditional probability of B given A. It is also called the likelihood.
P(B) is the prior or marginal probability of B, and acts as a normalizing constant.

Bayes' theorem in this form gives a mathematical representation of how the conditional probability of event A given B is related to the converse conditional probability of B given A.

Bayes' theorem with continuous prior and posterior distributions

Suppose a continuous probability distribution with probability density function ƒ_Θ is assigned to an uncertain quantity Θ. (In the conventional language of mathematical probability theory Θ would be a "random variable") The probability that the event B will be the outcome of an experiment depends on Θ; it is P(B | Θ). As a function of Θ this is the likelihood function:

$L(\theta) = P(B \mid \Theta = \theta). \,$

Then the posterior probability distribution of Θ, i.e. the conditional probability distribution of Θ given the observed data B, has probability density function

$f_\Theta(\theta \mid B) = \text{constant}\cdot f_\Theta(\theta) L(B \mid \theta), \,$

where the "constant" is a normalizing constant so chosen as to make the integral of the function equal to 1, so that it is indeed a probability density function. This is the form of Bayes' theorem actually considered by Thomas Bayes.

In other words, Bayes' theorem says:

To get the posterior probability distribution, multiply the prior probability distribution by the likelihood function and then normalize.

More generally still, the new data B may be the value of an observed continuously distributed random variable X. The probability that it has any particular value is therefore 0. In such a case, the likelihood function is the value of a probability density function of X given Θ, rather than a probability of B given Θ:

$L(\theta) = f_X(x \mid \Theta = \theta). \,$

A simple example of Bayes' theorem

Suppose there is a school with 60% boys and 40% girls as its students. The female students wear trousers or skirts in equal numbers; the boys all wear trousers. An observer sees a (random) student from a distance, and what the observer can see is that this student is wearing trousers. What is the probability this student is a girl? The correct answer can be computed using Bayes' theorem.

The event A is that the student observed is a girl, and the event B is that the student observed is wearing trousers. To compute P(A|B), we first need to know:

P(A), or the probability that the student is a girl regardless of any other information. Since the observers sees a random student, meaning that all students have the same probability of being observed, and the fraction of girls among the students is 40%, this probability equals 0.4.
P(B|A), or the probability of the student wearing trousers given that the student is a girl. Since they are as likely to wear skirts as trousers, this is 0.5.
P(B), or the probability of a (randomly selected) student wearing trousers regardless of any other information. Since half of the girls and all of the boys are wearing trousers, this is 0.5×0.4 + 1.0×0.6 = 0.8.

Given all this information, the probability of the observer having spotted a girl given that the observed student is wearing trousers can be computed by substituting these values in the formula:

$P(A|B) = \frac{P(B|A) P(A)}{P(B)} = \frac{0.5 \times 0.4}{0.8} = 0.25.$

Another, essentially equivalent way of obtaining the same result is as follows. Assume, for concreteness, that there are 100 students, 60 boys and 40 girls. Among these, 60 boys and 20 girls wear trousers. All together there are 80 trouser-wearers, of which 20 are girls. Therefore the chance that a random trouser-wearer is a girl equals 20/80 = 0.25. Put in terms of Bayes´ theorem, the probability of a student being a girl is 40/100, the probability that any given girl will wear trousers is 1/2. The product of these two is 20/100, but we know the student is wearing trousers, so one deducts the 20 students not wearing trousers, and then calculate a probability of (20/100)/(80/100), or 20/80.

It is often helpful when calculating conditional probabilities to create a simple table containing the number of occurrences of each outcome, or the relative frequencies of each outcome, for each of the independent variables. The table below illustrates the use of this method for the above girl-or-boy example

	Girls	Boys	Total
Trousers	20	60	80
Skirts	20	0	20
Total	40	60	100

Application of the theorem

As a formal theorem, Bayes' theorem is valid in all common interpretations of probability. However, frequentist and Bayesian interpretations disagree on how (and to what) probabilities are assigned. In the Bayesian interpretation, probabilities are rationally coherent degrees of belief, or a degree of belief in a proposition given a body of well-specified information.^[2] Bayes' theorem can then be understood as specifying how an ideally rational person responds to evidence.^[1] In the frequentist interpretation, probabilities are the frequencies of occurrence of random events as proportions of a whole. Though his name has become associated with subjective probability, Bayes himself interpreted the theorem in an objective sense.^[3]

Bayes' theorem was given additional prominence by a theorem by the physicist R.T. Cox which showed that any system of inference that fit certain requirements could be mapped onto probability.^[2]^[4] Bayes' Theorem has since found a wide variety of applications in science and engineering.^[2]

Bayes' theorem derived via conditional probabilities

To derive Bayes' theorem, start from the definition of conditional probability. The probability of the event A given the event B is

$P(A|B)=\frac{P(A \cap B)}{P(B)}.$

Equivalently, the probability of the event B given the event A is

$P(B|A) = \frac{P(A \cap B)}{P(A)}. \!$

Rearranging and combining these two equations, we find

$P(A|B)\, P(B) = P(A \cap B) = P(B|A)\, P(A). \!$

This lemma is sometimes called the product rule for probabilities. Discarding the middle term and dividing both sides by P(B), provided that neither P(B) nor P(A) is 0, we obtain Bayes' theorem:

$P(A|B) = \frac{P(B|A)\,P(A)}{P(B)}. \!$

Of course, this lemma is symmetric in A and B, since A and B are arbitrarily-chosen symbols, and dividing by P(A), provided that it is non-zero, gives a statement of Bayes' theorem in which the two symbols have changed places.

Alternative forms

Bayes' theorem is often completed by noting that, according to the Law of total probability,

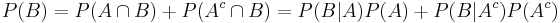$P(B) = P(A\cap B) + P(A^c\cap B) = P(B|A) P(A) + P(B|A^c) P(A^c) \!$ ,

where A^c is the complementary event of A (often called "not A").

This results in the analogous form:

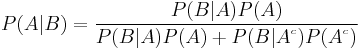$P(A|B) = \frac{P(B|A) P(A)}{P(B|A) P(A) + P(B|A^{^c}) P(A^{^c})} \!$ .

More generally, the law states that given a partition, i.e. {A_i}, of the event space

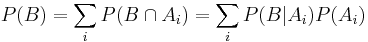$P(B) = {\sum_i P(B \cap A_i)} = {\sum_i P(B|A_i) P(A_i)} \!$ .

Thus, for any A_i in the partition, Bayes' theorem states that

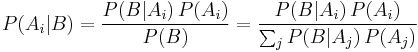$P(A_i|B) = \frac{P(B | A_i)\, P(A_i)}{P(B)} = \frac{P(B | A_i)\, P(A_i)}{\sum_j P(B|A_j)\,P(A_j)} \!$ .

In terms of odds and likelihood ratio

Bayes' theorem can also be written neatly in terms of a likelihood ratio Λ and odds O as

$O(A|B)=O(A) \cdot \Lambda (A|B)$

where O(A|B) are the (posterior) odds of A given B,

$O(A|B)=\frac{P(A|B)}{P(A^{^c}|B)} \!$

O(A) are the (prior) odds of A by itself

$O(A)=\frac{P(A)}{P(A^{^c})} \!$

and Λ(A|B) is the likelihood ratio.

$\Lambda (A|B) = \frac{P(B|A)}{P(B|A^c)} \!$

For probability densities

There is also a version of Bayes' theorem for continuous distributions. It is somewhat harder to derive, since probability densities are not probabilities, so Bayes' theorem has to be established by a limit process; see Papoulis's textbook (cited below), Section 7.3 for an elementary derivation.

Bayes originally used the theorem to find a continuous posterior distribution given discrete observations.

Bayes' theorem for probability densities is formally similar to the theorem for probabilities:

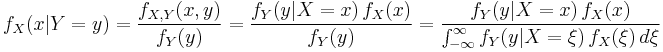$f_X(x|Y=y) = \frac{f_{X,Y}(x,y)}{f_Y(y)} = \frac{f_Y(y|X=x)\,f_X(x)}{f_Y(y)} = \frac{f_Y(y|X=x)\,f_X(x)}{\int_{-\infty}^{\infty} f_Y(y|X=\xi )\,f_X(\xi )\,d\xi }\!$ .

There is an analogous statement of the law of total probability, one which is used in the denominator:

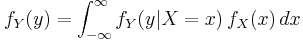$f_Y(y) = \int_{-\infty}^{\infty} f_Y(y|X=x )\,f_X(x)\,dx \!$ .

As in the discrete case, the terms have standard names.

$f_{X,Y}(x,y)\,$

is the joint density function of X and Y,

$f_X(x|Y=y)\,$

is the posterior probability density function of X given Y = y,

$f_Y(y|X=x) = L(x|y)\,$

is (as a function of x) the likelihood function of X given Y = y, and

$f_X(x)\,$

and

$f_Y(y)\!$

are the marginal probability density functions of X and Y respectively, where ƒ_X(x) is the prior probability density function of X.

Extensions

Theorems analogous to Bayes' theorem cover more than two events. For example:

$P(A|B \cap C) = \frac{P(A) \, P(B|A) \, P(C|A \cap B)}{P(B) \, P(C|B)}\,.$

This can be derived in a few steps from Bayes' theorem and the definition of conditional probability:

$P(A|B \cap C) = \frac{P(A \cap B \cap C)}{P(B \cap C)} = \frac{P(C|A \cap B) \, P(A \cap B)}{P(B) \, P(C|B)} = \frac{P(A) \, P(B|A) \, P(C|A \cap B)}{P(B) \, P(C|B)}\,.$

Similarly,

$P(A|B \cap C) = \frac{P(B|A \cap C) \, P(A|C)}{P(B|C)}\,$

can be regarded as a conditional Bayes' Theorem and can be derived as follows:

$P(A|B \cap C) = \frac{P(A \cap B \cap C)}{P(B \cap C)} = \frac{P(B|A \cap C) \, P(A|C) \, P(C)}{P(C) \, P(B|C)} = \frac{P(B|A \cap C) \, P(A|C)}{P(B|C)}\,.$

A general strategy is to work with a decomposition of the joint probability, and to marginalize (integrate or sum) over the variables that are not of interest. Depending on the form of the decomposition, it may be possible to prove that some integrals must be 1, and thus they fall out of the decomposition; exploiting this property can reduce the computations very substantially. A Bayesian network, for example, specifies a factorization of a joint distribution of several variables in which the conditional probability of any one variable given the remaining ones takes a particularly simple form (see Markov blanket).

Further examples

Example 1: Drug testing

An example of the use of Bayes' theorem is the evaluation of drug test results. Suppose a certain drug test is 99% sensitive and 99% specific, that is, the test will correctly identify a drug user as testing positive 99% of the time, and will correctly identify a non-user as testing negative 99% of the time. This would seem to be a relatively accurate test, but Bayes' theorem can be used to demonstrate the relatively high probability of misclassifying non-users as users. Let's assume a corporation decides to test its employees for drug use, and that only 0.5% of the employees actually use the drug. What is the probability that, given a positive drug test, an employee is actually a drug user? Let "D" stand for being a drug user and "N" indicate being a non-user. Let "+" be the event of a positive drug test. We need to know the following:

P(D), or the probability that the employee is a drug user, regardless of any other information. This is 0.005, since 0.5% of the employees are drug users. This is the prior probability of D.
P(N), or the probability that the employee is not a drug user. This is 1 − P(D), or 0.995.
P(+|D), or the probability that the test is positive, given that the employee is a drug user. This is 0.99, since the test is 99% accurate.
P(+|N), or the probability that the test is positive, given that the employee is not a drug user. This is 0.01, since the test will produce a false positive for 1% of non-users.
P(+), or the probability of a positive test event, regardless of other information. This is 0.0149 or 1.49%, which is found by adding the probability that a true positive result will appear (= 99% x 0.5% = 0.495%) plus the probability that a false positive will appear (= 1% x 99.5% = 0.995%). This is the prior probability of +.

Given this information, we can compute the posterior probability P(D|+) of an employee who tested positive actually being a drug user:

$\begin{align}P(D|+) & = \frac{P(+ | D) P(D)}{P(+)} \\ & = \frac{P(+ | D) P(D)}{P(+ | D) P(D) + P(+ | N) P(N)} \\ & = \frac{0.99 \times 0.005}{0.99 \times 0.005 + 0.01 \times 0.995} \\ & = 0.3322.\end{align}$

Despite the specificity and sensitivity of the test, the low base-rate of use renders the accuracy of the test low: the probability that an employee who tests positive actually using drugs is only about 33%, so it is in fact more likely that the employee is not a drug user. The rarer the condition for which we are testing, the greater the percentage of positive tests that will be false positives.

We can also compute the posterior probability P(N|+) probabiliy of an employee who tested positive actually being a non-drug user.

$\begin{align}P(N|+) & = \frac{P(+ | N) P(N)}{P(+)} \\ & = \frac{P(+ | N) P(N)}{P(+ | N) P(N) + P(+ | D) P(D)} \\ & = \frac{0.01 \times 0.995}{0.99 \times 0.005 + 0.01 \times 0.995} \\ & = 0.6678.\end{align}$

The result shows that there is a 66.78% chance that an employee who tested positive is a non-user, despite the specificity and sensitivity of the test being 99%.

Example 2: Bayesian inference

Main article: Bayesian inference

Applications of Bayes' theorem often assume the philosophy underlying Bayesian probability that uncertainty and degrees of belief can be measured as probabilities.

We describe the marginal probability distribution of a variable A as the prior probability distribution or simply the "prior" distribution. The conditional distribution of A given the "data" B is the posterior probability distribution or just the "posterior" distribution.

Suppose we wish to know about the proportion r of voters in a large population who will vote "yes" in a referendum. Let n be the number of voters in a random sample (chosen with replacement, so that we have statistical independence) and let m be the number of voters in that random sample who will vote "yes". Suppose that we observe n = 10 voters and m = 7 say they will vote yes. From Bayes' theorem we can calculate the probability distribution function for r using

$f(r | n=10, m=7) = \frac {f(m=7 | r, n=10) \, f(r)} {\int_0^1 f(m=7|r, n=10) \, f(r) \, dr}. \!$

From this we see that from the prior probability density function f(r) and the likelihood function L(r) = f(m = 7|r, n = 10), we can compute the posterior probability density function f(r|n = 10, m = 7).

The prior probability density function f(r) summarizes what we know about the distribution of r in the absence of any observation. We provisionally assume in this case that the prior distribution of r is uniform over the interval [0, 1]. That is, f(r) = 1. If some additional background information is found, we should modify the prior accordingly. However before we have any observations, all outcomes are equally likely.

Under the assumption of random sampling, selecting voters is just like getting random balls from an urn. The likelihood function L(r) = P(m = 7|r, n = 10,) for such a problem is just the probability of 7 successes in 10 trials for a binomial distribution.

$P( m=7 | r, n=10) = {10 \choose 7} \, r^7 \, (1-r)^3.$

As with the prior, the likelihood is open to revision—more complex assumptions will yield more complex likelihood functions. Maintaining the current assumptions, we compute the normalizing factor,

$\begin{align} \int_0^1 P( m=7|r, n=10) \, f(r) \, dr & = \int_0^1 {10 \choose 7} \, r^7 \, (1-r)^3 \, 1 \, dr \\ & = {10 \choose 7} \left / {11 \choose 3,7,1} \right . = {10 \choose 7} \, \frac{1}{1320} \end{align}$

and the posterior distribution for r is then

$f(r | n=10, m=7) = \frac{{10 \choose 7} \, r^7 \, (1-r)^3 \, 1} {{10 \choose 7} \, \frac{1}{1320}} = 1320 \, r^7 \, (1-r)^3$

for 0 ≤ r ≤ 1.

One might be interested in the probability that more than half the voters will vote "yes". The prior probability that more than half the voters will vote "yes" is 1/2, by the symmetry of the uniform distribution. In comparison, the posterior probability that more than half the voters will vote "yes", i.e., the conditional probability given the outcome of the opinion poll – that seven of the 10 voters questioned will vote "yes" – is

$1320\int_{1/2}^1 r^7(1-r)^3\,dr \approx 0.887, \!$

which is about an "89% chance".

Example 3: The Monty Hall problem

Main article: Monty Hall problem

We are presented with three doors — red, green, and blue — from which to choose, one of which has a prize hidden behind it. Suppose we choose the red door. The host of the contest, who knows the location of the prize and will not open that door, opens the blue door and reveals that there is no prize behind it. He then asks if we wish to change from our initial choice of red. Will changing to green now improve our chances of winning the prize?

One may think, with two doors left unopened, that one has a 50:50 chance with either one, so there is no point for or against changing doors. However, this is not true.

Let us call the situations where the prize is behind one of the doors door A_r, A_g, and A_b, for the red, green, and blue doors, respectively. It is commonly assumed the car is placed randomly, hence

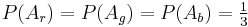$P(A_r) = P(A_g) = P(A_b) = \tfrac 13$ .

Let us call "the host opens the blue door" proposition B. It is assumed the host choose at random when he has a choice, hence B must have probability 1/2.

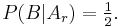
When the prize is behind the red door, the host is free to open the green or the blue door. If the host opens them uniformly at random: $P(B|A_r) = \tfrac 12.$

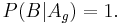
When the prize is behind the green door, the host must open the blue door. Thus: $P(B|A_g) = 1.$

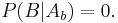
When the prize is behind the blue door, the host must open the green door. Thus, $P(B|A_b) = 0.$

Thus, under the condition we have chosen the red door, we get:

$\begin{align} P(A_r|B) & = \frac{P(B | A_r) P(A_r)}{P(B)} = \frac{\frac 1 2 \cdot \frac 13}{\frac 12} = \tfrac 13 \\ P(A_g|B) & = \frac{P(B | A_g) P(A_g)}{P(B)} = \frac{1 \cdot \frac 13}{\frac 12} = \tfrac 23 \\ P(A_b|B) & = \frac{P(B | A_b) P(A_b)}{P(B)} = \frac{0 \cdot \frac 13}{\frac 12} = 0 \end{align}$

So, we should change from the red to the green door for the higher probability of winning.

All of this assumes that after we have chosen a door, the host opens a second door at random, with equal probability, whenever two are available: the rooms behind both the green and blue doors are empty because behind the red door is the prize. If the host always opens the blue door in that situation, it makes no difference what we do. If the host never opens the blue door when the rooms behind both the green and blue doors are empty, then we with certainty will get the prize by changing from red to green. Under these two alternative assumptions, "always" and "never", the unconditional probability that the host opens the blue door happens to be 2/3 and 1/3, rather than 1/2 as above.

Historical remarks

Bayes' theorem was named after the Reverend Thomas Bayes (1702 - 61), who studied how to compute a distribution for the probability parameter of a binomial distribution (in modern terminology). His friend Richard Price edited and presented this work in 1763, after Bayes' death, as An Essay towards solving a Problem in the Doctrine of Chances.^[5] The French mathematician Pierre-Simon Laplace reproduced and extended Bayes' results in 1774, apparently quite unaware of Bayes' work.

Bayes presented his work as the solution to a problem:

Given the number of times in which an unknown event has happened and failed [... Find] the chance that the probability of its happening in a single trial lies somewhere between any two degrees of probability that can be named.^[5]

Bayes gave an example of a man trying to guess the ratio of "blanks" and "prizes" at a lottery. So far the man has watched the lottery draw 10 blanks and one prize. Given these data, Bayes showed in detail how to compute the probability that the ratio of blanks to prizes is between 9:1 and 11:1 (the probability is low - about 7.7 percent). Bayes went on to describe that computation after the man has watched the lottery draw 20 blanks and two prizes, 40 blanks and four prizes, and so on. He ends with the lottery having drawn 10,000 blanks and 1,000 prizes. The resulting probability is quite high - about 0.97 - that the ratio of blanks to prizes is between 9:1 and 11:1.^[5]

One of Bayes's results (Proposition five) gives a simple description of conditional probability, and it shows that conditional probability can be expressed independently of the order of events:

"If there be two subsequent events, the probability of the second b/N and the probability of both together P/N, and it being first discovered that the second event has also happened, from hence I guess that the first event has also happened, the probability I am right is P/b."

In modern terms, P/b = P(A| B) where A and B are the first and second subsequent events -- or the conditional probability of the first event where the condition is that the second event has happened. The expression says nothing about the order of occurrence: it measures correlation, and not causation.

Bayes's preliminary results, in particular Propositions three, four, and five imply the truth of the theorem that is named for him, but it does not appear that Bayes emphasized or focused on that finding.

Bayes' main result (Proposition nine in the essay) is the following in modern terms: Assume a uniform prior distribution of the binomial parameter p. After observing m successes and n failures, the probability that p is between two values a and b is this.

$\frac {\int_a^b {n+m \choose m} p^m (1-p)^n\,dp} {\int_0^1 {n+m \choose m} p^m (1-p)^n\,dp} \!$

What is "Bayesian" about Proposition nine is its presentation as a probability about the parameter p, a probability in this case. One may compute the probabilities for an experimental outcome, of course, but one may also do it for the parameter which governs it, and the same algebra and calculations are used to make inferences of both kinds.

Bayes stated his question in a way that may make assigning a probability distribution to a parameter palatable to a "frequentist". He supposed that a billiard ball is thrown at random onto a billiard table, and that p and q = (1 - p) are the probabilities that further billiard balls will fall above or below the first ball.

Stephen Fienberg describes the evolution from "inverse probability" at the time of Bayes and Laplace, a term still used by Harold Jeffreys (1939), to "Bayesian" in the 1950s.^[6] Ironically, Ronald A. Fisher introduced the "Bayesian" label in a derogatory sense. It is unclear whether Bayes was Bayesian in the modern sense. That is, whether he was interested in inference, or rather, merely in probability. The essay of 1763 is more of a paper on probability.

Stephen Stigler suggested in 1983 that Bayes' theorem was discovered by Nicholas Saunderson some time before Bayes.^[7] Edwards (1986) disputed that interpretation.^[8]

Richard Price and the Existence of a Deity

Richard Price discovered Bayes's essay and its now-famous theorem in Bayes's papers after Bayes' death. He believed that Bayes' Theorem helped prove the existence of God ("the Deity") and wrote the following in his introduction to the Essay.

The purpose I mean is, to shew what reason we have for believing that there are in the constitution of things fixt laws according to which things happen, and that, therefore, the frame of the world must be the effect of the wisdom and power of an intelligent cause; and thus to confirm the argument taken from final causes for the existence of the Deity. It will be easy to see that the converse problem solved in this essay is more directly applicable to this purpose; for it shews us, with distinctness and precision, in every case of any particular order or recurrency of events, what reason there is to think that such recurrency or order is derived from stable causes or regulations in nature, and not from any irregularities of chance. --Philosophical Transactions of the Royal Society of London, 1763.^[5]

References

↑ ^1.0 ^1.1 Howson, Colin; Peter Urbach (1993). Scientific Reasoning: The Bayesian Approach. Open Court. ISBN 9780812692341.
↑ ^2.0 ^2.1 ^2.2 ^2.3 Jaynes, Edwin T. (2003). Probability theory: the logic of science. Cambridge University Press. ISBN 9780521592710.
↑ Earman, John (1992). "Bayes' Bayesianism". Bayes Or Bust?: A Critical Examination of Bayesian Confirmation Theory. MIT Press. ISBN 9780262050463.
↑ Baron, Jonathan (1994). Thinking and Deciding (2 ed.). Oxford University Press. pp. 209–210. ISBN 0521437326.
↑ ^5.0 ^5.1 ^5.2 ^5.3 Bayes, Thomas, and Price, Richard (1763). "An Essay towards solving a Problem in the Doctrine of Chance. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, M. A. and F. R. S.". Philosophical Transactions of the Royal Society of London 53: 370–418. doi:10.1098/rstl.1763.0053. http://www.stat.ucla.edu/history/essay.pdf.
↑ Fienberg, Stephen E. (2006).When Did Bayesian Inference Become “Bayesian”?.
↑ Stephen M. Stigler (1983), "Who Discovered Bayes' Theorem?" The American Statistician 37(4):290–296.
↑ A. W. F. Edwards (1986), "Is the Reference in Hartley (1749) to Bayesian Inference?", The American Statistician 40(2):109–110

Versions of the essay

Bayes, Thomas; Price, Mr. (1763). "An Essay towards solving a Problem in the Doctrine of Chances.". Philosophical Transactions of the Royal Society of London 53: 370–418. doi:10.1098/rstl.1763.0053.
Barnard, G (1958). "Studies in the History of Probability and Statistics: IX. Thomas Bayes's Essay Towards Solving a Problem in the Doctrine of Chances". Biometrika 45 (3–4): 296–315.. doi:10.1093/biomet/45.3-4.293.
Thomas Bayes "An essay towards solving a Problem in the Doctrine of Chances". (Bayes' essay in the original notation)

Commentaries

G. A. Barnard (1958) "Studies in the History of Probability and Statistics: IX. Thomas Bayes' Essay Towards Solving a Problem in the Doctrine of Chances", Biometrika 45:293–295. (biographical remarks)
Daniel Covarrubias. "An Essay Towards Solving a Problem in the Doctrine of Chances". (an outline and exposition of Bayes' essay)
Stephen M. Stigler (1982). "Thomas Bayes' Bayesian Inference," Journal of the Royal Statistical Society, Series A, 145:250–258. (Stigler argues for a revised interpretation of the essay; recommended)
Isaac Todhunter (1865). A History of the Mathematical Theory of Probability from the time of Pascal to that of Laplace, Macmillan. Reprinted 1949, 1956 by Chelsea and 2001 by Thoemmes.
Eliezer S. Yudkowsky (2003). An Intuitive Explanation of Bayesian Reasoning (includes Java applets and biography)

Additional material

Pierre-Simon Laplace (1774/1986), "Memoir on the Probability of the Causes of Events", Statistical Science 1(3):364–378.
Stephen M. Stigler (1986), "Laplace's 1774 memoir on inverse probability", Statistical Science 1(3):359–378.
Jeff Miller, et al., Earliest Known Uses of Some of the Words of Mathematics (B). (very informative; recommended)
Athanasios Papoulis (1984), Probability, Random Variables, and Stochastic Processes, second edition. New York: McGraw-Hill.
The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J. C. MacKay provides an up to date overview of the use of Bayes' theorem in information theory and machine learning.
Bayes' Theorem entry by James Joyce in the Stanford Encyclopedia of Philosophy, provides a comprehensive introduction to Bayes' theorem.
Stanford Encyclopedia of Philosophy: Inductive Logic provides a comprehensive Bayesian treatment of Inductive Logic and Confirmation Theory.
Weisstein, Eric W., "Bayes' Theorem" from MathWorld.
Bayes' theorem at PlanetMath.
Eliezer S. Yudkowsky (2003), "An Intuitive Explanation of Bayesian Reasoning"
A tutorial on probability and Bayes’ theorem devised for Oxford University psychology students
Confirmation Theory An extensive presentation of Bayesian Confirmation Theory